Section 1.2/1.3: Slope Fields and Solutions

Slope Fields and Solution Curves

Slope Field: An Ordinary Differential Equation (ODE) of the form \(\frac{dy}{dx} = f(x,y)\) specifies a slope value (from left to right) at each point in the \((x,y)\)-plane.

Solution Curve: A curve in the \(xy\)-plane whose derivatives "follow the slope field" determined by the ODE.

Example: \(y' = x - y\)

Document: Slope Fields and Solutions (Page 1)

Image 1: Slope Field for \(y' = x - y\)

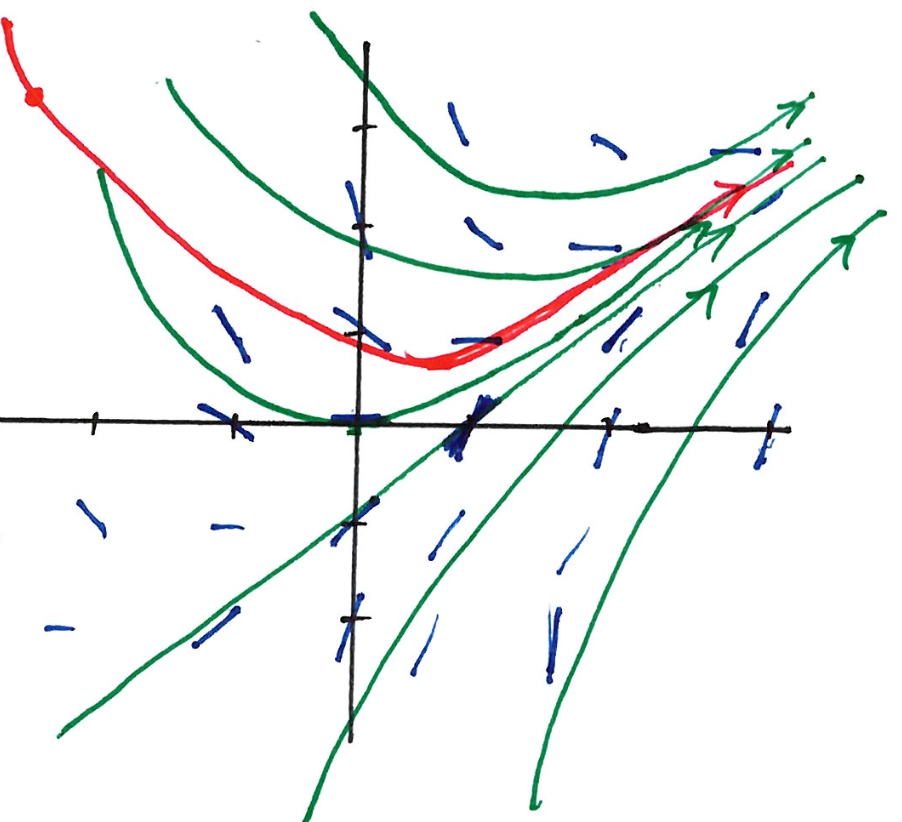
<p><strong>Description:</strong> </p> <p>A coordinate plane showing a slope field where small line segments represent the tangent slope at various points \((x, y)\). The slopes follow the function \(f(x, y) = x - y\).</p> <ul> <li><strong>General Solutions:</strong> Multiple green curves are sketched across the plane, flowing in the direction of the slope segments. These curves converge toward a diagonal path as \(x\) increases.</li> <li><strong>Particular Solution (IVP):</strong> A single prominent red curve is highlighted. This curve specifically passes through the point \((-4, 3)\), representing the solution to the Initial Value Problem \(y' = x - y\) with \(y(-4) = 3\).</li> </ul>
  • The green curves represent various general solution curves.
  • Initial Value Problem (IVP): To find a specific curve, we use an initial value such as \(y(-4) = 3\).
  • The red curve represents the unique solution passing through the point \((-4, 3)\).

Classifying Solutions

1. General vs. Particular

  • General Solution: Includes an unknown constant \(C\).
    • Example: \(y = x^2 + C\) is the general solution for \(y' = 2x\).
  • Particular Solution: A solution where the constant \(C\) has been determined, usually by an initial condition.
    • Example: \(y = x^2 + 7\) is the particular solution for the IVP \(\{y' = 2x, y(0) = 7\}\).

2. Explicit vs. Implicit

  • Explicit Solution: The dependent variable is isolated, e.g., \(y = f(x)\).
    • Example: \(y = \tan(4x^3 + C)\).
  • Implicit Solution: The solution is given as a relationship between variables, e.g., \(F(x,y) = C\).
    • Example: \(x^2 + y^2 = C\).

Note: You can verify an implicit solution using implicit differentiation. For \(x^2 + y^2 = C\):

\[2x + 2yy' = 0 \implies y' = -\frac{x}{y}\]

Matching ODEs to Slope Fields

To identify an ODE from a slope field, analyze where the slopes are zero, positive, or negative.

Description: A slope field visualization used for a matching exercise. The segments show the following characteristics: Equilibrium Lines: At \(y = 3\) and \(y = 0\), the slope segments are perfectly

Step-by-Step Analysis

  1. Find Equilibria: Observe where the slopes are horizontal (\(y' = 0\)). In this field, this occurs at \(y = 0\) and \(y = 3\).
  2. Check Regions:
    • For \(y > 3\): The slopes are positive (increasing).
    • For \(0 < y < 3\): The slopes are negative (decreasing).
    • For \(y < 0\): The slopes are positive (increasing).
  3. Test Equations:
    • Consider \(y' = y(y - 3)\).
      • If \(y=4\): \(4(4-3) = +4\) (Matches).
      • If \(y=1\): \(1(1-3) = -2\) (Matches).
      • If \(y=-1\): \(-1(-1-3) = +4\) (Matches).

Result: The slope field corresponds to the differential equation \(y' = y(y - 3)\).